SISTEMA DE REFERENCIA EL SALVADOR (II): FÓRMULAS DE CONVERSIÓN
En nuestra última entrada empezamos a conocer los parámetros que definen un sistema de referencia de coordenadas (CRS) y mas especificamente dimos a conocer los parámetros que se utilizan para el sistema de referencia de El Salvador.
En la entrada de ahora vamos a ver las fórmulas que sirven para convertir coordenadas de un sistema a otro y así poder configurarlas en una hoja de cálculo como en Excel, si no tuvieramos tanta experiencia en Sistemas de Información Geográfica que es donde vamos a explicar como hacerlo en nuestra próxima entrada.

PARÁMETROS DE LA PROYECCIÓN
Para comenzar definamos la simbología a utilizar para las fórmulas, el significado de cada una de estas variables fue explicado en la entrada anterior asi que si hubiera alguna duda pueden regresar a ella a consultar. En una tercera columna se han colocado los valores para nuestro SRC.
| a | Semieje del Elipsoide de referencia | 6 378 137 m |
| f | Achatamiento elipsoidal | 1/298.257 222 101 |
| ϕ1 | Latitud del primer paralelo estándar | 13° 19′ 03.477624″ N |
| ϕ2 | Latitud del segundo paralelo estándar | 14° 15′ 03.477624″ N |
| ϕ0 | Latitud origen | 13° 47′ 03.477624″ N |
| λ0 | Longitud origen | 88° 59′ 59.938692″W |
| N0 | Falso Norte | 295809.184 m |
| E0 | Falso Este | 500000.000 m |
| FE | Factor de escala | 0.99996704 |
| ϕ | Latitud conocida a convertir | |
| λ | Longitud conocida a convertir | |
| N | Norte conocido a convertir | |
| E | Este conocido a convertir |
CONSTANTES DE LA PROYECCIÓN

Antes de poder realizar la conversión de sistemas de referencia se necesitan calcular algunos parámetros adicionales a definir a continuación.




Donde:


m1 y m2 se obtienen evaluando m con ϕ1 y ϕ2 respectivamente.
t0, t1 y t2 se obtienen evaluando t con ϕ0, ϕ1 y ϕ2 respectivamente.
CONVIRTIENDO COORDENADAS GEOGRÁFICAS A PROYECCIÓN CÓNICA COMFORME DE LAMBERT
La conversión de coordenadas geográficas ( ϕ , λ ) a coordenadas proyectadas (N, E) se realiza en varios pasos.
Primero hay que determinar t y ρ usando la latitud conocida a convertir ( ϕ ) y las fórmulas previamente presentadas. Luego se evalua ɣ en la longitud conocida a convertir ( λ ) usando:

Entonces la proyección Norte (N) y Este (E) se calcula como :


Las coordenadas obtenidas con las fórmulas anteriores deberán de ser multiplicadas por el factor de escala FE para poder tener las coordenadas exactas del punto.
CONVIRTIENDO COORDENADAS PROYECTADAS A GEOGRÁFICAS
La conversión de coordenadas proyectadas (N,E) a geográficas se realiza en varios pasos, comenzando con los siguientes cálculos:

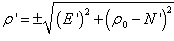
El signo de la formula anterior debe de ser igual al obtenido para el valor de n.


La latitud a calcular se determina de manera iterativa. Una primera aproximación se logra con la siguiente formula:

Luego ϕ se sustituye en la siguiente fórmula:

El valor calculado se va sustituyendo en la fórmula hasta que la diferencia es casi nula, normalmente eso pasa luego de 3 iteraciones
La longitud del punto es detemrinada como

Esperamos que esta entrada haya sido interesante para ti y que hayas aprendido mucho. Si hubiera alguna pregunta, no dudes en dejarla en los comentarios, más abajo o a través de nuestras redes sociales y a la mayor brevedad posible las estaremos respondiendo. Si esta entrada te ha gustado te invitamos a que la compartas para que este conocimiento llegue a más personas. Hasta la próxima
Otras entradas que te pueden interesar:
- Consultoría de catastro multifinalitario El Salvador
- ¿Qué es la Topología?
- Control de verticalidad con apoyo topográfico
- Usando LiDAR para descubrir sitios arqueológicos en El Salvador
- La costa salvadoreña en un mapa científico francés del siglo XVIII.