¿Por qué las elevaciones de GPS no sirven para los proyectos de obra civil? Altitudes ortometricas y elipsoidales
*Por Edgard Granados
Lo vamos a ver aparecer en todos los términos de referencias o especificaciones técnicas de los proyectos: hay que establecer una red de control en el proyecto con sistema GNSS pero la indicación es clara, las elevaciones de los puntos de control no pueden ser elipsoidales. ¿Qué significa esto?

Este artículo es continuación de un artículo que escribimos la semana pasada y que pueden leer aquí.
Comencemos por una definición más básica: en Geomática altura y elevación no es lo mismo. Altura hace referencia a la diferencia de elevación entre el comienzo y el fin de un objeto en particular, por ejemplo, la altura de un edificio. Elevación o altitud es la diferencia que hay desde una superficie geodésica de referencia por ejemplo el Geoide o el Elipsoide.

Una vez definido el Geoide como la superficie equipotencial de referencia, será importante definir cómo medir las elevaciones respecto a esta superficie y como se relacionan con otras figuras geodésicas como el elipsoide.
La nivelación geométrica está basada en la utilización del instrumento conocido como nivel que a través de su visual genera una superficie tangente al punto donde se encuentra el aparato o lo que es lo mismo una normal a la vertical del lugar.
Conociendo las lecturas sobre la estadia se pueden calcular las diferencias de elevación entre dos puntos, y podríamos decir que esta es la separación entre dos superficies equipotenciales Wa y Wb. En distancias cortas la variación de la distancia entre las superficies equipotenciales resulta irrelevante.
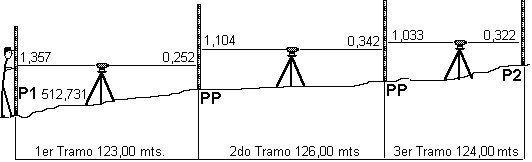
Cuando la distancia entre puntos a nivelar es muy grande se deberán de realiza varias estaciones entre A y B y considerar la variación entre superficies equipotenciales, tal como se muestra en la siguiente figura.
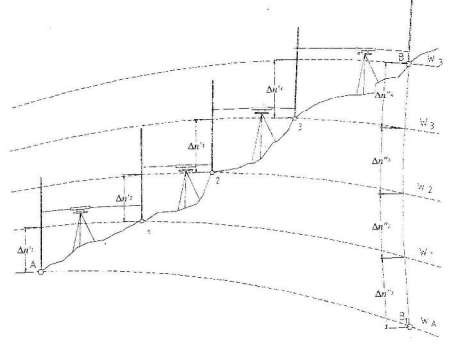
De la figura anterior se puede observar que conociendo la elevación del punto A, la elevación del punto B no será la misma si se realiza un itinerario del tipo AB o del tipo AB1B. Para el caso la segunda opción la altitud será mayor a pesar de que el desplazamiento se ha dado sobre la línea equipotencial donde se encuentra A.

COTA GEOPOTENCIAL
El concepto de nivel se puede asociar también al concepto de potencial gravitatorio, es decir, puntos que estén a mayor elevación tienen un potencial gravitatorio mayor.
Definiendo como superficie equipotencial de referencia al geoide con potencial W0 se define como cota geopotencial del punto P al resultado de la siguiente expresión:
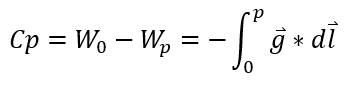
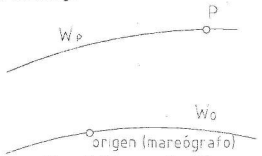
La ventaja de definir esta variable es que es independiente del camino que se recorra, para todos los casos se tiene un valor único. Sin embargo, no representa una dimensión física si no el trabajo que el trabajo necesario para trasladar una masa unitaria desde el origen hasta un punto P.
Si se discretiza la formula anterior para poder aplicarla en términos prácticos, y considerando una referencia de cota geopotencial desde un punto que no necesariamente el geoide obtenemos:
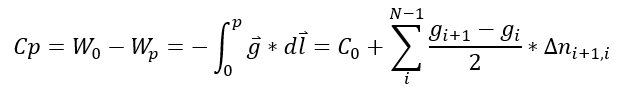
Las unidades de la cota geopotencial son Kgal x m.
COTA DINAMICA
La cota dinámica es la división de la cota geopotencial entre el valor de la gravedad normal para 45° de latitud, por convención, para poder obtener valores de altitud geométrica como tal.
¿Por que 45° de latitud? Pues no hay ningun lugar que lo diga explicitamente pero no es casualidad que EEUU y muchos paises de Europa tengan 45° de latitud.
Matemáticamente se define como:
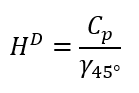
ELEVACIONES ORTOMETRICAS
Se define como altitud o elevacion ortométrica de un punto a la distancia entre dicho punto y el geoide medida según la dirección de la vertical (la dirección perpendicular al geoide).
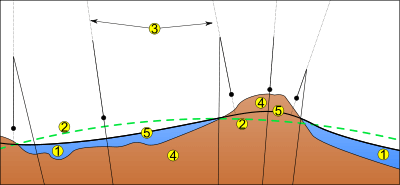
Para poder explicar de manera grafica, conceptual y matemáticamente se coloca nuevamente aquí la siguiente figura

De la figura anterior la elevacion ortométrica viene representado por la suma de los desniveles entre las distintas superficies equipotenciales desde el punto B1 hasta B.
Con base en la definición discreta de la cota geopotencial, y recordando que el cálculo de ésta es independiente del camino se pueden realizar las siguientes deducciones:
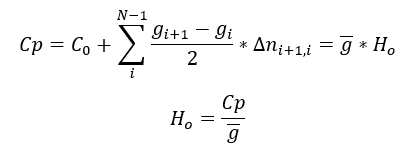
Es importante señalar que en la formula anterior la gravedad promedio a calcular es la que hay en la dirección del perpendicular al geoide y esto representa un problema pues no es posible determinarla de forma inmediata.
Para resolver el problema anterior Herlmert, utilizando una reducción de Poincaré Preg propone calcular la elevacion ortométrica como se indica a continuación:
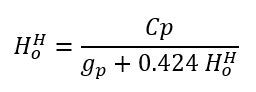
La fórmula anterior puede resolverse por métodos iterativos o resolviendo la formula cuadrática implícita.
ALTITUDES NORMALES
Una alternativa para la resolución de la altitud considerando las limitaciones de las altitudes ortométricas es calcular las altitudes normales, las cuales se calculan igual que las altitudes ortometricas con la diferencia que se asume que la gravedad promedio viene dado por la gravedad normal en ese punto.
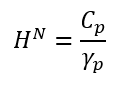
RELACION CON LAS ALTITUDES ELIPSOIDALES (GPS)
Actualmente, con las ventajas que ofrece la medición con sistemas de posicionamiento por satélite es posible determinar las posiciones de un punto en la tierra ocupando el sistema de referencia WGS84. El problema es que la altitud obtenida por estos métodos es una altitud de tipo elipsoidal, es decir, medida sobre el elipsoide y desde que el elipsoide es una modelación matemática de la tierra las altitudes elipsóidicas no tienen significación física.
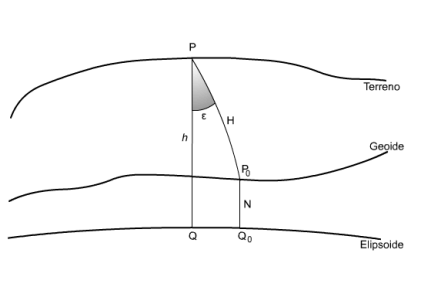
Así la elevacion elipsoidal, considerando algunas simplificaciones podrá relacionarse con la ondulación del geoide (N) con la siguiente relación:
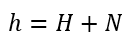
En resumen, la referencia de elevación no se ha cambiado en relación al concepto que sabemos desde pequeños, que la altura se mide en el sentido de la vertical, es decir, en el sentido de la gravedad; pero en grandes dimensiones la gravedad se ve influida por la distribución no uniforme de masas de la Tierra y que la forma en que se vería una superficie de igual gravedad le llamamos Geoide pero que es muy difícil de modelar porque es muy irregular y por ello creamos el Elipsoide como una figura matemática con la cual es más fácil calcular posiciones y que por tanto es más fácil de ocupar con los GPS pero las elevaciones del GPS son de tipo elipsoidales y habrá que corregirlas al Geoide que si es la verdadera manera en la que se mide la vertical.
Esperamos que esta entrada haya sido interesante para ti y que hayas aprendido mucho. Si hubiera alguna pregunta, no dudes en dejarla en los comentarios, más abajo o a través de nuestras redes sociales y a la mayor brevedad posible las estaremos respondiendo. Si esta entrada te ha gustado te invitamos a que la compartas para que este conocimiento llegue a más personas. Hasta la próxima
Otras entradas que te pueden interesar:
- Consultoría de catastro multifinalitario El Salvador
- ¿Qué es la Topología?
- Control de verticalidad con apoyo topográfico
- Usando LiDAR para descubrir sitios arqueológicos en El Salvador
- La costa salvadoreña en un mapa científico francés del siglo XVIII.
SOBRE EL AUTOR
ELLOS YA CONFÍAN EN NUESTRA EXPERIENCIA Y CALIDAD

DEJANOS TUS COMENTARIOS Y SÍGUENOS EN NUESTRAS REDES SOCIALES: