Planta eólica Ventus: Levantamiento As Built Línea de interconexión eléctrica
El proyecto de medición de la línea eléctrica y de interconexión Planta Eólica Ventus-Central Guajoyo fue todo un reto operativo, logístico, técnico y hasta matemático y en esta entrada vamos a hablar como logramos realizar este proyecto

El proyecto “Línea de Interconexión 115kV – Parque Eólico Ventus” contempla la construcción y puesta en marcha de una Línea de Interconexión de 115Kv, de aproximadamente 22.5km de longitud, medidos desde la Subestación de Transformación en el municipio de Metapán, hasta la subestación Central Hidroeléctrica Guajoyo.
La línea amarilla al centro de la siguiente imagen muestra el trazo general de la línea de interconexión a lo largo del municipio de Metapán.
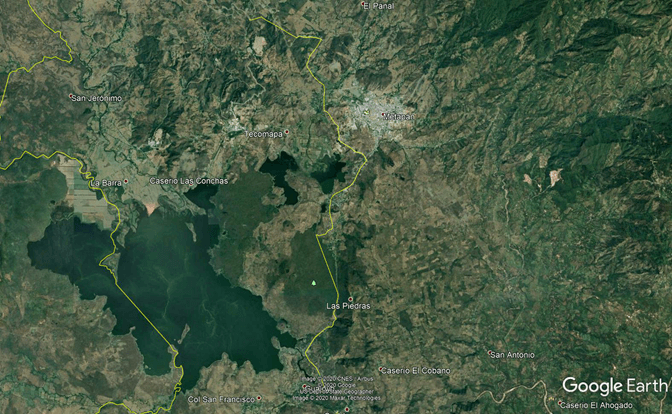
El objetivo el levantamiento as built consistía, entre otras cosas, realizar la determinación de los siguientes parámetros:
- Determinación de la verticalidad de los 163 postes que componen la línea
- Determinar la separación de la línea y los postes con otras líneas eléctricas tanto en horizontal como en vertical
- Determinar la distancia que hay de las estructuras a las calles, ejes de calles y cercos o líneas de linderos más cercanos
- Determinación de los libramientos de la catenaria de las líneas
EQUIPO Y HERRAMIENTAS UTILIZADAS
Para la realización de las mediciones de datos en campo se utilizó una estación total marca CYGNUS modelo 2LS que cuenta con la ventaja de poder tomar datos en cualquier tipo de superficie y no únicamente con el prisma de reflexión.

A continuación, se presentan las especificaciones técnicas más importantes del equipo relacionada con las labores realizadas para el proyecto.


Todos los datos de los postes, a excepción de la elevación de la base, fueron medidos con la estación total en modo “Non-prism Fine” lo que garantiza que los datos se devuelven con precisión milimétrica y con un error de +/- 3 mm + 2 ppm (2 mm por cada kilómetro de separación entre la estación y el punto que se ha medido) lo cual se considera como una tolerancia admisible para el diámetro y tamaño de los detalles a medir.
El equipo de trabajo en campo estuvo compuesto por un total de 3 personas, uno desarrollándose como topógrafo y los otros 2 como auxiliares o también conocidos como cadeneros.

METODOLOGÍA DE CAMPO
A continuación, se explicarán las diferentes metodologías adoptas en campo para la captura de datos necesarios para la determinación de los datos objetivos del proyecto.
DATOS MEDIDOS PARA LA DETERMINACIÓN DE LA VERTICALIDAD DE LAS ESTRUCTURAS
Para la determinación de la verticalidad de postes se realizó la medición de 3 puntos por cada una de las secciones del poste. Como se explicará más adelante esto se hizo así para poder cumplir con el mínimo de puntos necesarios para la determinación de la circunferencia.
A continuación, se presenta una imagen muestra tomada de los archivos entregados donde presenta de manera puntual la aplicación del guardado de información comentado previamente.
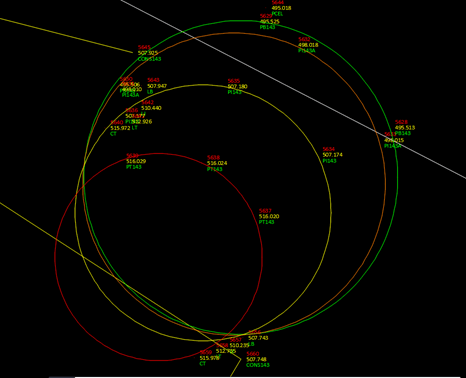
MEDICIÓN DE LÍNEAS
Para la explicación de la metodología de campo para la determinación de la información referente a las líneas eléctricas que hay entre estructuras se dividirá en 2 partes: la determinación de puntos de entrada y salida de las líneas y la metodología para la medición de información para catenarias y libramientos.
MEDICIÓN DE ENTRADAS Y SALIDAS DE LÍNEAS EN POSTES
El proceso realizado para le medición del punto de entrada y salida de las líneas fue ocupar la opción de medición sin prisma (Non prism mode) para medir el punto en que las líneas pasan en los postes.
MEDICIÓN DE LIBRAMIENTOS EN LÍNEAS
Para la determinación de la ecuación de la catenaria (más detalle en la sección “Determinación de la ecuación de la catenaria por series de potencia y mínimos cuadrados”) se realizó la medición de puntos por debajo de la línea utilizando el siguiente procedimiento:
- Ubicación del cadenero debajo de la línea
El primer paso realizado por el equipo de trabajo fue que el cadenero se ubicó en puntos por debajo de la línea de interconexión alineando la línea definida por parte larga de la tarjeta del prisma con la línea que definían los cables de la línea de interconexión, con esta manera asegurábamos que nos encontrásemos exactamente debajo de los cables.
El común denominador fue tomar 3 puntos lo más equiespaciados en los tramos de la línea, sin embargo, es importante señalar que en tramos cortos se tomó la decisión de tomar únicamente 1 o 2 puntos intermedios, según la longitud de la línea, lo cual sigue siendo suficiente para la definición de la curva catenaria según se explicará en la sección respectiva.

Para la medición de estos puntos intermedios se utilizó un modo de la estación total que se conoce como “Medición de elevación remota” en la cual se mide a un prima con bastón colocados a nivel de terreno natural y justamente por debajo del punto de interés y se colima o visualiza posteriormente el punto objetivo.
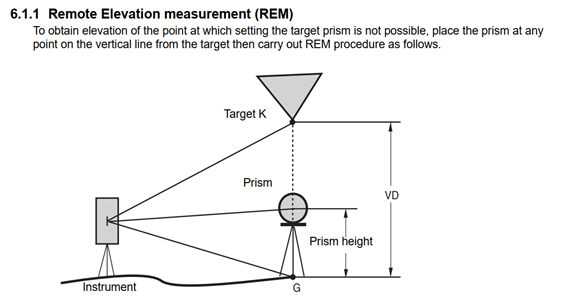
CONCEPTOS UTILIZADOS PARA EL ANÁLISIS Y PROCESAMIENTO DE LA INFORMACIÓN
Esta sección tiene por objetivo presentar de manera resumida pero concisa los conceptos utilizados para el procesamiento de los datos tomados en campo y que se calculan de manera automática a través de las hojas de cálculo compartidas en los productos entregables.
ECUACIÓN GENERAL DE LA CIRCUNFERENCIA
El procedimiento normalmente utilizado para la determinación de la verticalidad de los postes es realizar la medición de puntos sobre una dirección entre poste y estación total y luego realizar el mismo procedimiento a 90° sobre ese punto. Sin embargo, debido a la altura de los postes (30 m en el peor de los casos) y que la estación total únicamente permite visualizar lo que se mide hasta un ángulo cenital de 45° aproximadamente (lo que significa que se debía estar a más de 30 m de los postes para poder visualizar cómodamente la parte más alta) y las limitantes de campo (cercanía a construcciones, cercos y similares en la mayoría de los postes) era imposible realizar la medición con esta técnica.
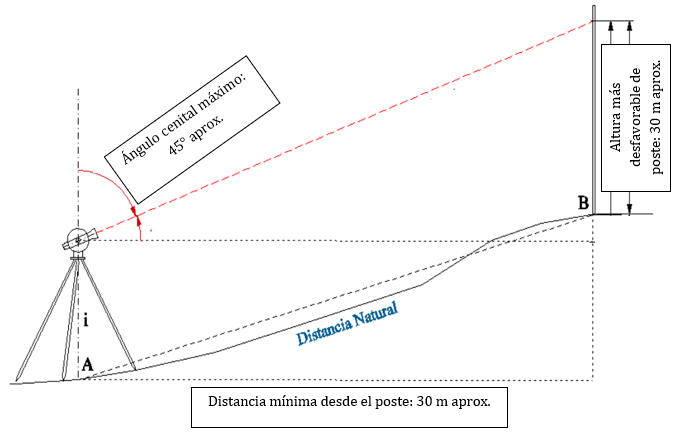
Para solventar esa limitante la estrategia que se adoptó fue medir, desde un solo punto de estación, 3 puntos cualesquiera, para una misma altura, que son los mínimos que se necesitan para definir una circunferencia.
En la ecuación general de la circunferencia los parámetros desconocidos son únicamente las constantes y son únicamente 3, así que para poder resolver las constantes se necesitan al menos 3 ecuaciones, para resolver las 3 incógnitas y por tanto 3 datos conocidos de la circunferencia para poder sustituirlos en la ecuación general.
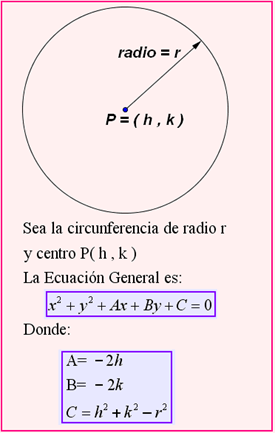
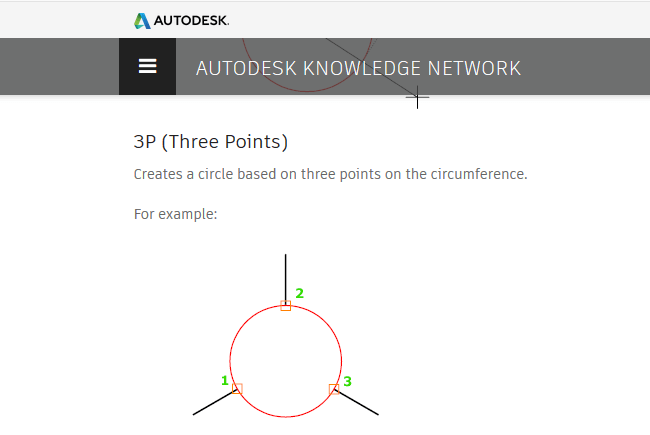
En AutoCAD existe la opción para poder dibujar una circunferencia teniendo 3 puntos conocidos, este comando basa su aplicación en los conceptos de la ecuación general discutidos previamente.
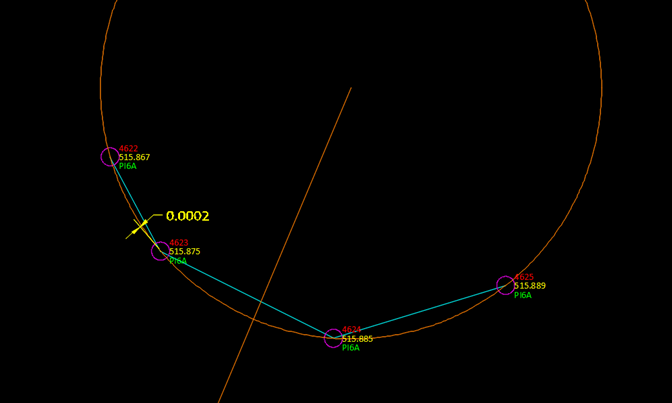
Para comprobar que el método se realizó la medición de algunos postes con 4 puntos, realizando la creación del círculo utilizando la opción antes mencionada y midiendo la diferencia que hay al 4° punto. Para el caso el error fue de 0.2 mm lo cual se considera aceptable tomando como base el ancho del poste.
DETERMINACIÓN DE LA BISECTRIZ POR MEDIO DE VECTORES UNITARIOS
Al menos en teoría el desplazamiento de los postes debería de darse en la dirección de la bisectriz de los postes que es la línea determinada por la mitad del ángulo que existe entre la línea de entrada y la de salida.
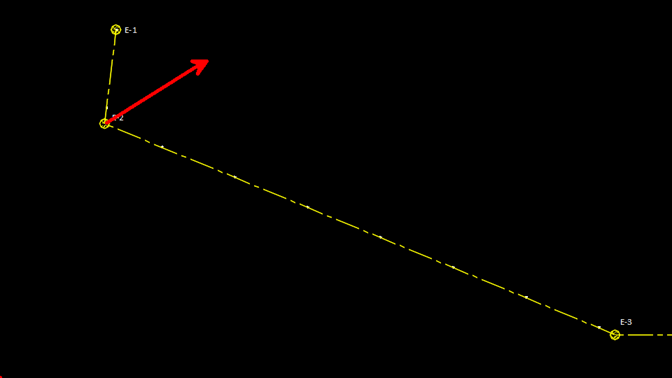
Para comprobar que el desplazamiento de los postes se estuviera dando en el sentido teórico fue necesario determinar el sentido el ángulo de la bisectriz y compararlo con el sentido de desplazamiento del poste.
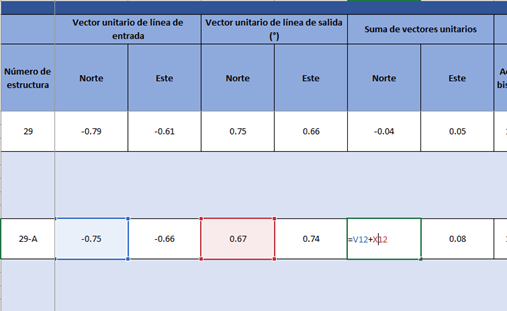
La dirección de la bisectriz viene marcada por el vector suma, siempre que los módulos de los dos vectores sumandos sean iguales. Bastará entonces encontrar dos vectores en la dirección de los dados, pero con el mismo módulo, por ejemplo, ambos unitarios, y hacer su suma.
La fórmula para la determinación del vector unitario se presenta a continuación:

Para la determinación de la bisectriz se calculó el vector unitario de la línea incidente y de la línea saliente pues se conocían los puntos de comienzo y de fin de cada uno de los tramos de la línea.
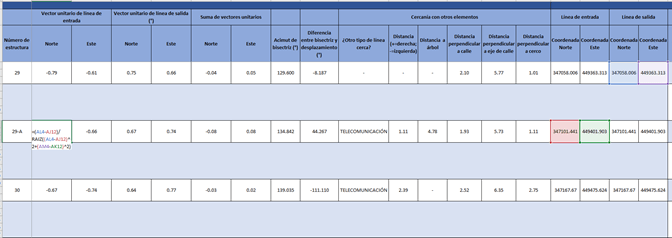
Sumando las respectivas componentes, cada una con su similar, se puede determinar las componentes del vector suma.
Y conociendo las componentes del vector suma se puede conocer su dirección. Es importante señalar que para poder estandarizar la dirección de la bisectriz se decidió calcular como un acimut. Un acimut es el ángulo que hay entre el Norte geográfico y la línea de interés. Así, todos los sentidos de las líneas de bisectrices e incluso los sentidos de los desplazamiento de los postes han sido referenciados al Norte Geográfico (acimutales).
DETERMINACIÓN DE LA ECUACIÓN DE LA CATENARIA POR SERIES DE POTENCIAS Y MÍNIMOS CUADRADOS
Un cable atado entre 2 puntos de densidad lineal constante sometido a un campo gravitatorio constante describe una trayectoria que se conoce como Catenaria.
Matemáticamente, y de forma más general, la catenaria se describe a través de un coseno hiperbólico con la siguiente expresión:
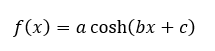
De donde se desconocen el valor de las constantes a, b y c que definen el desplazamiento de la catenaria desde los ejes y su concavidad.
Siendo que hay 3 incógnitas en la ecuación se necesitan al menos 3 ecuaciones para poder resolverla, estas ecuaciones son puntos donde se conocen los valores de X y de Y. Sin embargo, el simultaneo de ecuaciones no lineales es un proceso demasiado complicado para poder desarrollarse a través de una hoja de cálculo por lo que se decidió desarrollar el fórmula del coseno hiperbólico a través de su serie de potencias hasta el grado 2 para poder facilitar el simultaneo.
La serie de Taylor, es decir, la representación de la función centrada en los ejes es la siguiente:
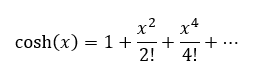
De forma más general la serie se puede aplicar a la ecuación general de la Catenaria mostrada previamente como:
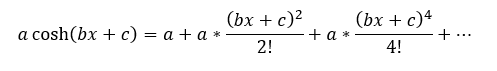
Si nos quedamos únicamente con los términos hasta el grado 2 y se desarrolla el producto notable de ese término se tiene:
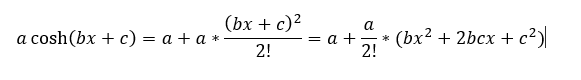
Puesto que a, b y c son constantes la multiplicación por otras constantes solo producirá otras constantes por lo que se puede simplificar la fórmula de la siguiente manera:
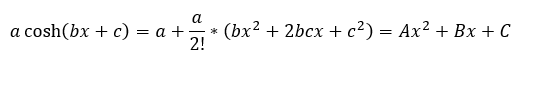
Quedando entonces una ecuación donde hay 3 incógnitas (A, B y C) y para la cual se necesitan únicamente 3 valores conocidos para determinar 3 ecuaciones.
Como se mencionó en la sección “MEDICIÓN DE LIBRAMIENTOS EN LÍNEAS” entre cada estructura, según la longitud, se midieron puntos intermedios para poder modelar la catenaria de la línea y como se estableció en el párrafo anterior se necesitan al menos 3 puntos para poder definirla, en los tramos pequeños los 3 puntos mínimos se cumplen considerando los puntos de entrada y salida del tramo de la línea y el punto que se tomó en el tramo. Sin embargo, en los tramos más largos y con el fin de poder modelar de mejor manera la línea de la catenaria se tomaron 3 puntos intermedios que junto con los puntos de entrada y de salida de la línea suman un total de 5 puntos disponibles para el modelado matemático.
Cuando se poseen más datos de los necesarios se necesita realizar un ajuste por mínimos cuadrados para poder ajustar los datos al modelo.
Un ajuste por mínimos cuadrados minimiza, como su nombre mismo lo dice, el cuadrado de los errores que hay entre el modelo y los datos medidos.

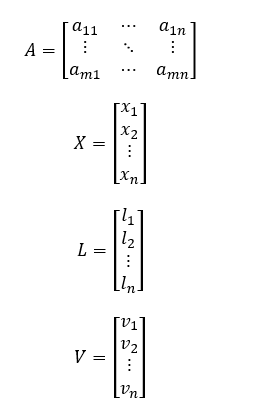
El método de mínimos cuadrados se puede calcular de forma matricial de manera más eficiente. Se establece una ecuación de la forma:
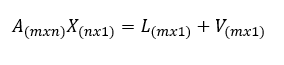
Donde:
- A= Matriz de coeficientes de incógnitas (valores de distancias , x y 1 definidas en la serie de potencias)
- X= Matriz de incógnitas (valores de constantes definidas en la serie de potencias)
- L=Matriz de observaciones (elevaciones de los cables medidas de campo)
- V= Matriz de residuos (diferencias entre el modelo y los datos medidos)
Para resolver la matriz X (incógnitas) se utiliza la siguiente expresión:
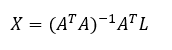
Y la matriz de residuos se calcula como:
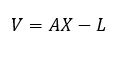
Una forma de verificar que el método es válido es viendo que en los tramos de línea donde se tienen los puntos mínimos (3) para realizar el modelado de la catenaria, los residuos de ese modelado son cero puesto que no hay margen de maniobra para el ajuste, la ecuación se calcula con los puntos mínimos y por tanto no hay ajuste.
Para encontrar el punto más bajo del tramo, teniendo ya definida la ecuación cuadrática de la línea en esa sección se derivó la ecuación e igualó a cero para encontrar su mínimo.

Para aquellos que estén interesados en profundidar en la aplicación de conceptos matemáticos en la Topografía les compartimos el siguiente video sobre una conferencia impartida por nuestro Director General sobre el tema
Otras entradas que te pueden interesar:
- Consultoría de catastro multifinalitario El Salvador
- ¿Qué es la Topología?
- Control de verticalidad con apoyo topográfico
- Usando LiDAR para descubrir sitios arqueológicos en El Salvador
- La costa salvadoreña en un mapa científico francés del siglo XVIII.
ELLOS YA CONFÍAN EN NUESTRA EXPERIENCIA Y CALIDAD

DEJANOS TUS COMENTARIOS Y SÍGUENOS EN NUESTRAS REDES SOCIALES: