Procesamiento digital de imágenes
*Por Edgard Granados
La fotografía digital revolucionó de muchas maneras las formas en las que la captura de imágenes podía ser utilizadas, y la geomática no escapó de ello.
Antes, al tomar una fotografía, un tinte especial sensitivo a la luz imprimía una imagen en una película en función de cómo la luz hiciera reaccionar esa tinta con base en el tiempo de abertura de la lente. El mismo principio se aplica para las cámaras digitales con la diferencia de que en lugar de existir una película son muchos pequeños sensores que captan como infiere la luz en la posición en la que están y el conjunto de todo eso genera una imagen.
El concepto anterior es básico para entender como la Geomática realiza análisis basado en imágenes digitales. Computacionalmente hablando una imagen es una matriz. Sin entrar en más detalles por el momento la forma más simple de entender una imagen digital es pensar que es como una cuadrícula con filas y columnas, cada posición fila-columna representa un pixel. Así, por ejemplo, una imagen de 12 megapíxeles quiere decir que está compuesta por 12 millones de posiciones. Aunque las combinaciones para formar esos 12 millones de posiciones pueden ser muchas, una forma fácil de entenderlo es con una fotografía de relación 3:4 una proporción bastante común hoy en día. En este tipo de fotografía hay 3,000 columnas y 4,000 filas, lo que conforma los 12 millones de posiciones posibles o sea los 12 millones de píxeles de la imagen.

Ahora bien, pongámoslo un poco más complicado. En términos digitales para formar un color se necesita la combinación, en mayor o menor proporción, de 3 colores básicos: Rojo, Azul y Verde (RGB) por tanto una imagen digital a color en realmente una matriz tridimensional de al menos 3 niveles. Una imagen de 12 megapíxeles con relación de forma 3:4 tendrá 3 matrices, una por cada valor RGB, de 3 mil columnas por 4 mil filas. Pero aquí es donde se complica aún más la cosa, en nuestra entrada de Teledetección explicamos que esta rama de la Geomática se ocupa de recolectar información en zonas del espectro electromagnético que no es posible visualizar con el ojo humano, pues éste solo puede ver en la zona del espectro de luz visible (normalmente constituido por la combinación de colores RGB en términos digitales), pero satélites como el americano Landsat, o el europeo Sentinel, tienen la posibilidad de capturar imágenes hasta en 11 bandas del espectro electromagnético, lo que quiere decir que digitalmente hablando esas imágenes son matrices al menos 11 niveles de profundidad y ni hablar de los satélites hiperespectrales que capturan más de 30 bandas de información.
Ahora bien, si alguna vez te has preguntado para qué aprendiste Álgebra Matricial en el colegio o en la Universidad y te costaba entender para que podría ser útil saber sumar, restar o invertir matrices, pues déjame decirte que hay un área de la Geomática que se llama «Procesamiento digital de imágenes» y pues como ya dijimos antes, las imágenes digitales son realmente matrices de valores digitales con diferentes niveles de profundidad (3 si hablamos de una imagen a color).
Este articulo también te servirá para entender cómo es que hace Instagram para aplicarle los filtros a las fotografías.

Para poner un ejemplo práctico de cómo es el procesamiento digital de imágenes vamos a ver uno de los múltiples análisis que se puede hacer con imágenes multiespectrales (muchas otras posibles combinaciones se pueden encontrar en nuestra entrada de teledetección).
El Índice de Vegetación Normalizada (NDVI, por sus siglas en inglés) es un índice utilizado para estimar la cantidad y calidad de un cultivo. En formula se calcula así:

Básicamente lo que la fórmula anterior dice es que todas las posibles bandas que pueda tener una imagen multiespectral habrá que restar la matriz de píxeles de la banda de infrarrojo cercano con la banda del rojo y ese resultado dividirlo por la suma de los píxeles de ambas bandas (recuerden que las imágenes multiespectrales se toman con cámaras especiales que capturan información más allá del espectro visible). Las imágenes de este ejemplo se muestran a continuación:
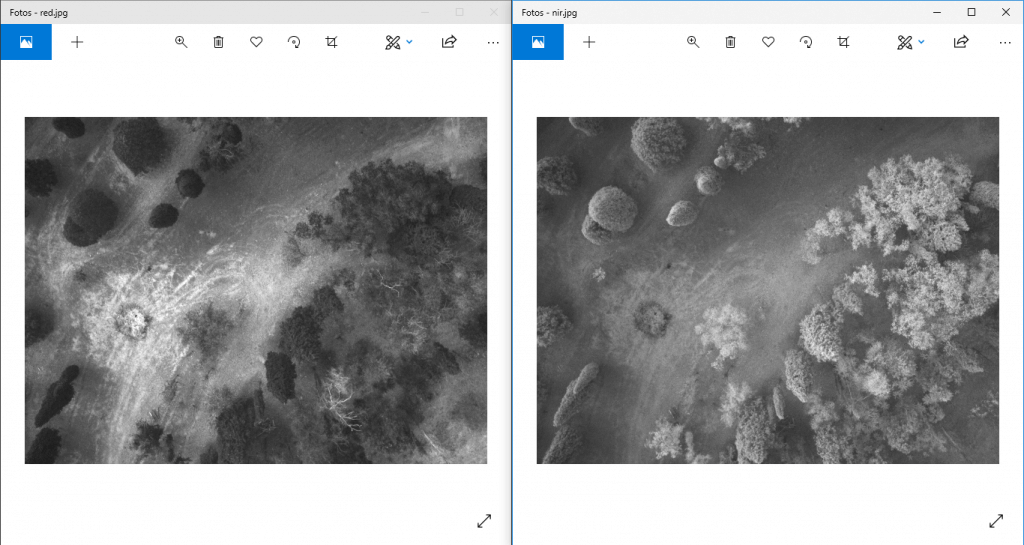
Recuerden que las imágenes anteriores se ven en blanco y negro porque el color se genera de la combinación de las bandas RGB, ahí lo que tenemos básicamente por cada imagen es una matriz de 1280×960 píxeles lo que constituye imágenes de 12 megapíxeles de resolución, cada píxel en cada imagen conteniendo información diferente, una los valores de rojo y otra los de infrarrojo pero al final con la misma resolución.
Pues bien, si se recuerdan de Álgebra Matricial para restar o sumar una matriz se hace la resta o la suma de cada elemento de una matriz con el elemento de la otra matriz en la misma posición. Todas las reglas del Álgebra Matricial son aplicables aquí, incluyendo las limitaciones de inversas y transpuestas y similares.
Para que los resultados de la operación tuvieran una mejor apreciación, nosotros creamos un programa en Matlab que luego de realizado el cálculo de NDVI y puesto que este índice toma valores entre -1 y 1 colocar un color visible en función del valor de NDVI.
A nivel general:
- Los valores negativos corresponden principalmente a las nubes, el agua y la nieve.
- Los valores cercanos a cero corresponden principalmente a rocas y terrenos desnudos o sin vegetación.
- Los valores por debajo de 0,1 corresponden a áreas yermas de rocas, arena o nieve.
- Los valores moderados (0,2 a 0,3) representan terrenos con arbustos y prados.
- Los valores altos indican bosques de zonas templadas y tropicales (0,6 a 0,8).
Los resultados del procesamiento de la imagen son los siguientes:
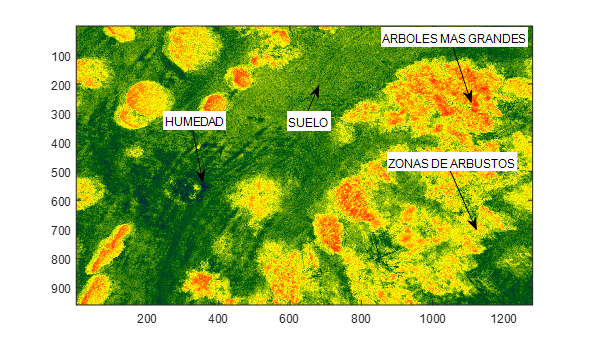

El anterior fue un ejemplo sencillo de procesamiento digital de imágenes, para a continuación les dejamos algunas posibles combinaciones de bandas que permiten visualizar información importante que sería invisible al ojo humano si no fuera por la combinación de bandas. Al final el concepto es el mismo: operaciones de álgebra matricial pues las imágenes digitales no son más que eso.
Espero que esta entrada haya sido interesante para ti y que hayas aprendido mucho. Si hubiera alguna duda no dudes en dejarla en los comentarios más abajo o a través de nuestras redes sociales que a la mayor brevedad posibles las estaremos respondiendo. Si te ha gustado te invito a que la compartas para que este conocimiento llegue a más y más personas. Hasta la próxima
Otras entradas que te pueden interesar:
- Consultoría de catastro multifinalitario El Salvador
- ¿Qué es la Topología?
- Control de verticalidad con apoyo topográfico
- Usando LiDAR para descubrir sitios arqueológicos en El Salvador
- La costa salvadoreña en un mapa científico francés del siglo XVIII.
SOBRE EL AUTOR
ELLOS YA CONFÍAN EN NUESTRA EXPERIENCIA Y CALIDAD

DEJANOS TUS COMENTARIOS Y SÍGUENOS EN NUESTRAS REDES SOCIALES: