Técnicas de observación de la tierra (III): ¿Cómo funciona un GPS?
Técnicas de observación de la tierra (III): ¿Cómo funciona un GPS?
La entrada del dia de ahora no es nueva en este blog. Ya hace algún tiempo escribimos una de nuestras primeras entradas explicando de manera sencilla cómo funciona un GPS así que el objetivo de hoy será meternos más en la matemática que hay detrás de los cálculos de GPS aunque con ciertos matices.

Puesto que el calculo de GPS puede volverse realmente complicado vamos a desglosar aquí como se realiza el calculo de posición de la manera mas simple cuando se utiliza un GPS. Si igual no es tu interés entrar en la matemática, o igual y quieres recordar los conceptos de una manera mas facil, aqui en seguida te dejo el link para que puedas leer nuestra entrada mas sencilla.
¿Cómo funciona un GPS? (Explicación sencilla)
PRINCIPIOS BÁSICOS DEL SISTEMA DE NAVEGACION POR SATELITE
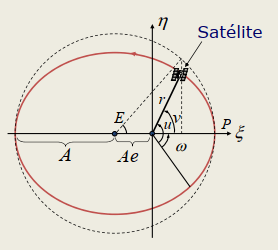
El principio básico de funcionamiento del sistema GNSS consiste en establecer la relación de vectores distancia que existen entre un receptor GNSS, el centro de masas de la tierra y el satélite de una constelación de posicionamiento global. La posición del satélite esta medida respecto al centro de masas de la tierra al igual que la posición del receptor GNSS, el cual es capaz de descifrar la señal electromagnética que emite el satélite y por tanto capaz de determinar el vector distancia satélite-receptor. Lo anterior se presenta en la siguiente imagen:
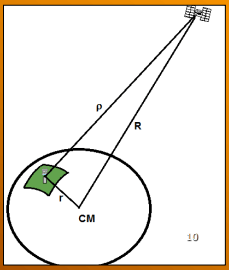
La determinación de la posición del satélite respecto al centro de masas de la tierra se realiza mediante la observación de cuásares en el espacio profundo que son objetos básicamente inmóviles, así el vector ‘r’ que es el vector incógnita puede determinarse con la resta vectorial del vector distancia receptor-satélite y CM-Satélite.

En la práctica para la determinación precisa de la posición de un receptor GNSS se utiliza la intersección de al menos 3 esferas con radio igual a la distancia determinada por la señal entre el receptor y el satélite. El volumen de intersección de las 3 esferas mínimas para la determinación de la posición es el espacio tridimensional que determina la precisión de la posición del receptor, es decir, es el volumen de incertidumbre de la posición. El concepto aplicado es que al definir una solo vector distancia entre un satélite un receptor genera un número de posibilidades de posición que se satisfacen para la ecuación de la esfera de radio igual al vector receptor-satélite, sin embargo, la posición del receptor es solo una de esas posibilidades. Si ahora se considera una segunda esfera desde otro satélite de la constelación, las opciones reducen únicamente al espacio tridimensional de la intersección de las esferas, pero no genera la solución para todas las posiciones espaciales del receptor, generando intersecciones con otras esferas de radio igual al vector distancia se van eliminando las posibilidades y se aceptan las que solo satisfacen los radios de todas las esferas a la vez. A continuación, se presenta un esquema que representa de manera gráfica la explicación anterior, para la intersección de 3 esferas:
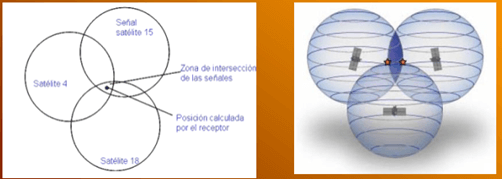
Aunque geométricamente es posible resolver la posición del receptor con la intersección de las 3 esferas será necesario disponer de, al menos, un cuarto satélite para determinar el estado del reloj del receptor. Esto es así, debido a que la precisión del reloj del receptor no es igual a la del satélite que lleva en su interior un reloj atómico de alta precisión.
Luego de considerar efectos ionosférico y troposféricos la ecuación para la determinación de la posición de un receptor respecto de la posición de un satélite en particular queda determinada por la siguiente ecuación:

MEDICIONES DE CODIGO: DESCRIPCION GEOMETRICA
INTRODUCCION
La determinación de la posición de un receptor utilizando medidas de código se basa en una multilateración tridimensional que sitúa al receptor en la intersección de unas esferas con centro en el satélite y de radio la distancia medida.
FUNCIONAMIENTO BASICO
El satélite emite un código que se repite con determinada frecuencia y a su vez cada receptor genera una réplica exacta de ese código. El receptor identifica el código mediante el mensaje de navegación y compara la señal recibida con la réplica del código generado en el instrumento. Cuando ambos códigos se encuentran perfectamente encajados se puede calcular un tiempo de retraso que permitirá calcular la distancia.
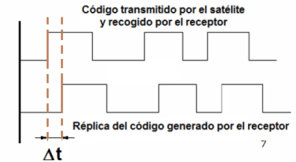
La intersección de 3 esferas obtenidas por observación a 3 satélites permitirá obtener la ubicación del receptor en la superficie terrestre.
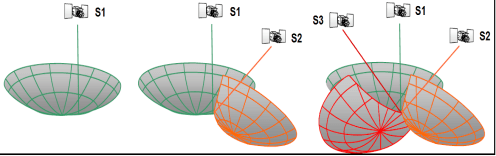
Sin embargo, será necesario disponer de un cuarto satélite para determinar el estado del reloj del receptor, esto debido a la diferencia de frecuencia de oscilación y por tanto la diferencia de precisión entre el reloj del receptor y del satélite siendo esta la cuarta incógnita del sistema.
Debido al diferente estado de los relojes del receptor y el satélite, el intervalo de tiempo medido en el reloj del receptor procedente de la correlación del código recibido y el generado proporcionará un valor falso del tiempo de transito de la señal.
Por tanto, también se obtendrá un valor erróneo de la distancia pasándose a denominar pseudo-distancia, quedando determinada por la siguiente ecuación:

MEDICIONES DE CODIGO: DESCRIPCION MATEMATICA
A la aproximación de distancia anterior habrá que añadirle los siguientes efectos si se quiere modelar correctamente la distancia existente entre el satélite y el receptor:

Quedando entonces la ecuación de pseudodistancias como sigue:
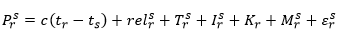
Si se expresa el tiempo de emisión en el satélite en función del tiempo de recepción de la señal en el receptor y se tienen en cuenta el estado del reloj del receptor y el estado del reloj del satélite se obtiene la siguiente expresión:
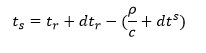
Siendo ⍴ la distancia calculada.
Sustituyendo la ecuación anterior en la fórmula simplificada de la ecuación de la pseudodistancia queda:
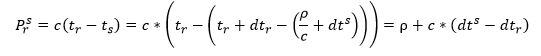
Así el cálculo simplificado de la pseudodistancia queda determinado por la distancia observada y los errores del receptor y el satélite, donde el error del receptor es incógnito del sistema y el del satélite se puede calcular con los datos que vienen datos en el fichero de navegación.
La expresión de la distancia receptor-satélite viene dada por:
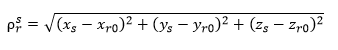
Los inconvenientes con esta expresión son:
- Se necesitan las coordenadas del satélite
- Se necesitan unas coordenadas aproximadas del receptor
- La ecuación de la distancia no es lineal, y por tanto habrá que llevar a cabo un proceso de linealización.
DETERMINACION DE LAS POSICIONES DE LOS SATELITES: LEYES DE KEPLER
De la ecuación anterior es evidente que será necesario la determinación de la posición del satélite para el cálculo y posterior resolución del sistema de ecuaciones que determinan la posición del receptor.
Puesto que los satélites se pueden considerar cuerpos celestes artificiales cumplirán con las leyes de Kepler para el movimiento de cuerpos celestes.
El movimiento de los cuerpos celestes fue estudiado y determinado en formulas por el astrónomo Johannes Kepler en 1600s. De manera breve las 3 leyes determinadas por Kepler son:
- Todos los planetas se desplazan alrededor del sol describiendo orbitas elípticas y el sol se encuentra en uno de los focos.
- El radio que une un planeta y el sol recorre áreas iguales en tiempos iguales
- Para cualquier planeta, el cuadrado de su periodo orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.[2]
Con base en las leyes de Kepler posición del satélite vendrá determinada por las ecuaciones y parámetros siguientes:
- Anomalía media (M)
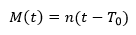
- Anomalía excéntrica (E)
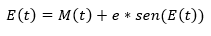
Donde e es la excentricidad de la órbita definida como la relación entre la distancia entre los focos y la del eje mayor
- Anomalía verdadera (v)
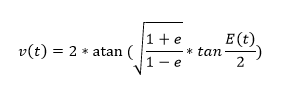
- Posición del cuerpo (r)
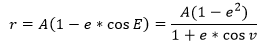
DETERMINACION DE LA POSICION DE LOS SATELITES
Para la determinación de las posiciones de satélites de manera más precisa se definen las siguientes constantes las cuales deben de ser introducidas como se muestran en los cálculos:
- Velocidad de la luz: c=2.99792458e8 m/s
- Constante gravitacional geocéntrica (GRS80) GM=3.9860050e14 m3/s2
- Constante de gravitación universal (WGS84) μ=3.9860050e14 m3/s2
- Velocidad de rotación de la tierra: ωe=7.2921151467e-5 m/s
- Constante relativista: F=-4.442807633e-10 s/m1/2
- Pi: π=3.1415926535898
Se deben de calcular las coordenadas que tiene el satélite en el instante en que se produce la recepción de la señal en el receptor. Estas serán las coordenadas del satélite que intervienen en las ecuaciones de la pseudodistancia.
Lo anterior es así pues desde que el satélite emite la señal hasta que llega al receptor, el satélite se ha desplazado varios cientos de metros. Además, durante ese intervalo de tiempo la tierra habrá rotado una variación angular que también se deberá de corregir.
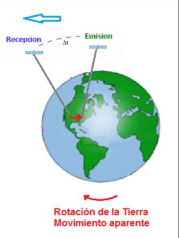
Demostración gráfica de la posición del receptor cuando emite y la posición del satélite cuando el receptor recibe la señal.
Respecto a la posición aproximada del receptor se introducirán coordenadas cercanas a la posición real. Sin embargo, esto no es del todo necesario debido a que el proceso de determinación de la posición se realizará por métodos iterativos por lo que cualquier terna de coordenadas funciona.
PRODUCTOS DEL IGS
El IGS recolecta, archiva y distribuye la serie de datos de observación GPS para satisfacer un amplio rango de aplicaciones y experimentos. Esta serie de datos son usados por el IGS para generar productos de datos los cuales son disponibles a través de internet.
El intervalo de publicación de las efemérides se muestra en la siguiente tabla.
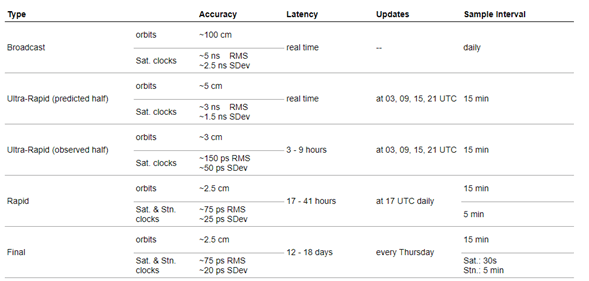
FORMATO SP3
El formato original del Standard Product 3 (SP3-a) fue propuesto en 1989, y modificado y adoptado hasta 1991. Este formato incluye datos tales como:
- Correcciones del reloj del satélite
- Exponentes de precisión de orbita
- Líneas de comentarios
- Semana GPS y segundos de la semana
- Una estructura de encabezado flexible
En 1998 se definió el formato SP3-b que permitía la combinación de las orbitas de satélite GPS con GLONASS. Actualmente se ocupa el formato SP3-c.
La estructura de dicho archivo puede consultarse en el siguiente enlace: ftp://igs.org/pub/data/format/sp3_docu.txt
Los archivos disponibles de descarga presentan el siguiente formato:
WWWW/AAAWWWWD.TYP.Z[6]
Donde:
| CODIGO | SIGNFICADO |
| WWWW | Semana GPS |
| AAA | Nombre del centro de análisis/Tipo de solución |
| D | Día de la semana (0-6) |
| HH | Hora |
| TYP | Tipo de solución |
| .Z | Extensión de archivo comprimido UNIX |
Para nuestro caso el tipo de solución que nos interesa son los archivos con extensión sp3. Estos archivos están disponibles para su descarga en el siguiente enlace: ftp://cddis.nasa.gov/gnss/products/
RINEX son las siglas en ingles de “Receiver INdependent Exchange”. Se trata de un formato de ficheros de texto orientado a almacenar, de manera estandarizada, medidas proporcionadas por los receptores de sistemas de navegación por satélite.[7]
La primera propuesta del formato RINEX fue desarrollada por el Instituto Astronómico de la Universidad de Berna para facilitar el intercambio de datos de GPS.[8]
Actualmente la versión de ficheros RINEX que se utilizan se encuentran en la versión 3.XX esta está compuesta por 3 ficheros del tipo ASCII:
- Fichero de observación
- Fichero de navegación
- Fichero meteorológico
Cada archivo está compuesto, en un principio, por un encabezado que contiene información general del fichero.
Un archivo RINEX, por convención, es nombrado de la siguiente forma:
SSSSDDDF.YYT
Donde:
- SSSS: Son los caracteres que representan el nombre de la estación
- DDD: Día del año, contando desde el primer dia del año
- F: Sesión
- YY: Los dos últimos dígitos del año
- T:
Tipo de fichero
- o: Observación
- n: Navegación
- m: Meteorológico
En este documento se dedicará únicamente al estudio de los componentes del archivo de navegación.
Se definen como efemérides, a la lista de posiciones de un objeto como una función de tiempo.[9] En el caso de los ficheros de navegación, las efemérides corresponden a los elementos que son necesarios para las ecuaciones de posición de los satélites.
Una estructura general de un fichero de navegación es como lo muestra la siguiente imagen, donde se puede ver claramente el encabezado y las efemérides de los satélites.
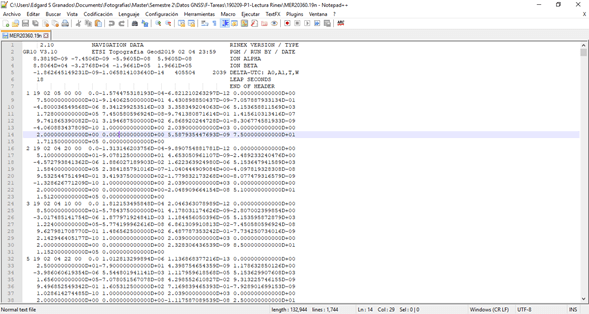
Como el objetivo principal es la familiarización de la estructura y lectura del fichero de navegación a continuación se enlistan los componentes del fichero mas no se explica en detalle el significado de cada uno el cual será discutido más adelante.
Los términos de los cuales están compuestos los ficheros de navegación son:
Tabla 1 Significado de siglas de elementos de un fichero de navegación
| ID | Numero PRN del satélite |
| Semana | Semana del GPS |
| toe | Época de referencia de las efemérides |
| sqrt(A) | Raíz cuadrada del semieje mayor |
| e | Excentricidad |
| M0 | Anomalía media en la época de la referencia |
| ω0 | Argumento del perigeo |
| i0 | Inclinación |
| Ω | Longitud del nodo ascendente |
| Δn | Diferencia de movimiento medio |
| IDOT | Velocidad del Angulo de inclinación |
| ΩDOT | Velocidad del nodo ascendente |
| Cuc Cus | Coeficientes de corrección del argumento del perigeo |
| Crc Crs | Coeficientes de corrección de la distancia geométrica |
| Cic Cis | Coeficientes de corrección de la inclinación |
| toc | Época de referencia para el reloj |
| a0 | Compensación del reloj |
| a1 | Deriva del reloj |
| a2 | Variación de la deriva |
Como ya se mencionó previamente, los ficheros RINEX son ficheros con un formato estandarizado para la facilitación de su lectura. A continuación, se presenta una tabla que muestra la distribución estándar de los datos de efemérides para un ejemplo general. Se presenta la abreviatura o sigla del elemento, el significado puede consultarse en la Tabla 1, y las unidades de cada uno de los elementos si es que corresponde.
En la discusión teórica de la práctica se introdujo una tabla con los parámetros que están contenidos en el fichero RINEX y que sirven para el cálculo de coordenadas.
Para la determinación de la posición de los satélites se detallan las siguientes formulas:
DIFERENCIA DE TIEMPO DESDE LA EPOCA DE REFERENCIA DE LAS EFEMERIDES (tk)
El primer paso es determinar la diferencia de tiempo desde la época de referencia de las efemérides (tk). Esto es, la diferencia entre el tiempo al cual se quiere determinar la posición del satélite (t), pero medido desde el tiempo de origen de las efemérides, menos el tiempo de origen de las efemérides (toe).
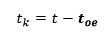
Una forma alternativa de cálculo es determinar cuanta fracción de día, en segundos, ha pasado desde el tiempo de origen de las efemérides y restarlo de la hora en la que se quiere determinar la posición del satélite. Esto lo que hace es evitar el cálculo de determinar que día de la semana es en la fecha y hora en la cual se quiere determinar la posición y calcular su tiempo desde el toe. El cálculo es como sigue:
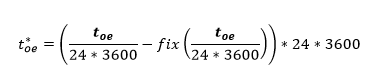
Así la diferencia de tiempo desde la época de referencia de las efemérides (tk) queda definida como:
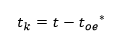
ANOMALIA MEDIA
No posee ningún significado físico, es solo un cálculo intermedio para cálculos posteriores.
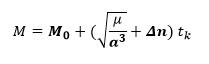
ANOMALIA EXCENTRICA
Es el ángulo medido en el plano orbital y desde el centro de la órbita.
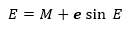
Sin embargo, como se puede ver esta forma es recursiva por lo que en principio se sugiere realizar un proceso de iteración considerando E0=0.
ARGUMENTO DE LONGITUD
Esta constituida por la Anomalía verdadera, que es la posición instantánea del satélite con respecto al perigeo, y el argumento del perigeo (ω)
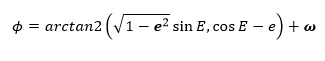
CORRECCIONES DE PERTURBACIONES DE SEGUNDOS ARMONICOS
Se divide en 3 partes:
- Argumento de la corrección de latitud
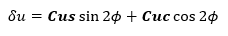
- Corrección radial
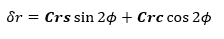
- Corrección de inclinación
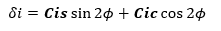
ARGUMENTO CORREGIDO DE LATITUD
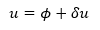
RADIO CORREGIDO
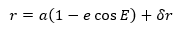
INCLINACIÓN CORREGIDA

LONGITUD CORREGIDA DEL NODO ASCENDENTE
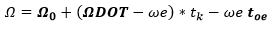
POSICIONES

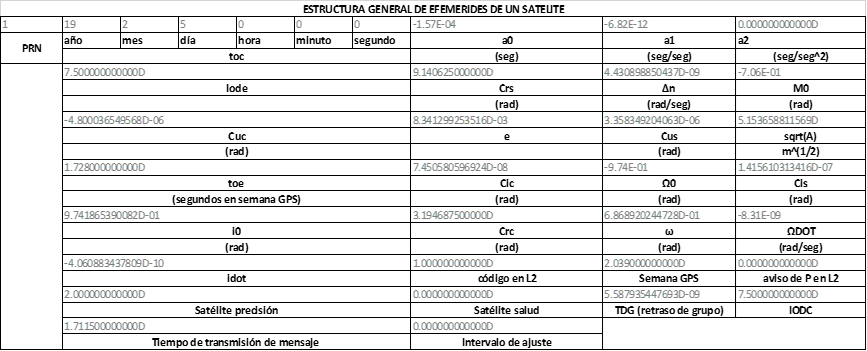
ERROR DEL RELOJ
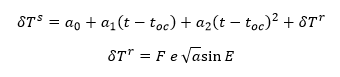
La linealización de la ecuación de distancias observadas se realiza a través de un desarrollo en series de potencias de la siguiente forma:
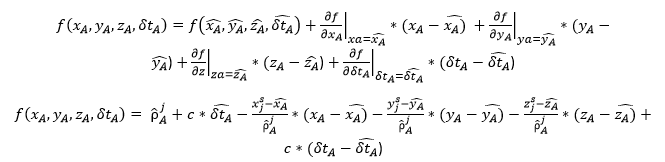
Así, reordenando los términos podemos escribir la ecuación general de posición en los siguientes términos:
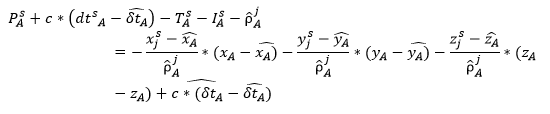
En términos matriciales se puede expresar como:
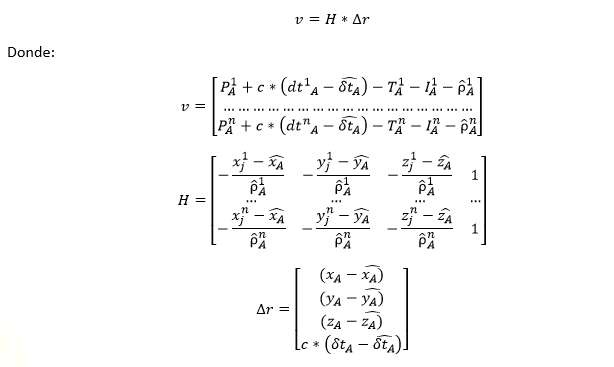
Debido al número de incógnitas en el sistema el menor número de satélites, como ya se había mencionado, deberá de ser 4.
El sistema se resuelve con un proceso iterativo en el cual:
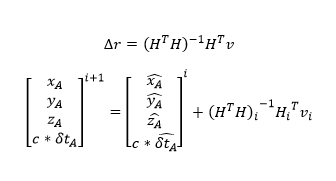
Otras entradas que te pueden interesar:
- Consultoría de catastro multifinalitario El Salvador
- ¿Qué es la Topología?
- Control de verticalidad con apoyo topográfico
- Usando LiDAR para descubrir sitios arqueológicos en El Salvador
- La costa salvadoreña en un mapa científico francés del siglo XVIII.
SOBRE EL AUTOR
ELLOS YA CONFÍAN EN NUESTRA EXPERIENCIA Y CALIDAD

DEJANOS TUS COMENTARIOS Y SÍGUENOS EN NUESTRAS REDES SOCIALES: