Geoestadística (III): Kriging
Hoy terminamos nuestra serie de Geoestadística con el que quizás es el método de interpolación más completo y utilizado por los especialistas para inferir datos de índole espacial son base en datos puntuales.
Las bases del Krigeado se deben al Ingeniero de minas Daniel Gerhardus Krige que en 1951 se planteó una solución al problema de estimar la distribución espacial de contenido de oro en las minas de Sudáfrica. Sin embargo, no fue hasta 20 años después que Georges Matheron y su grupo de investigación de la Escuela de Minas de París quienes formalizaron, desarrollaron y dieron el nombre al método.

El krigeado es una técnica de estimación que proporciona un estimador lineal insesgado y un error de estimación conocido como varianza de krigeado que depende del variograma y la ubicación de los datos. En otras palabras, la interpolación es de tipo lineal no afectada por algún error de tipo sistemático (insesgado) basado en la relación entre los datos puntuales (obtenidos del variograma).
Ahora bien, ya tocamos uno de los elementos más importantes para realizar el análisis del Kriging: el variograma. El variograma es una herramienta que permite analizar el comportamiento espacial de una variable sobre una zona dada. Es decir, estable la fuerza de la relación entre los valores puntuales de una zona.
Matemáticamente el variograma es el valor promedio de la diferencia al cuadrado de los valores de una propiedad de interés entre dos puntos separados una distancia h. Dicho de otra forma es como varían los valores de una variable (temperatura, contaminación, valor del suelo, etc.) en una determinada dirección.

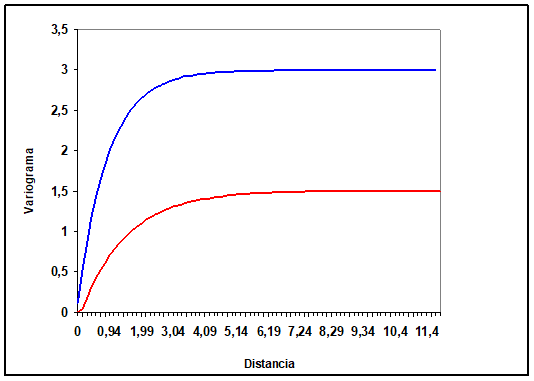
La forma más común de un variograma es la que aparece en la siguiente imagen. Para realizarlo hay que calcular el valor de la mitad de la diferencia de los valores para una distancia h y se va graficando consecutivamente esa distancia versus el valor

La forma anterior nos dice que a medida que la distancia (h) aumenta, la relación entre los puntos que se separan a esa distancia se empieza a estabilizar. Es decir, que a medida que los puntos se separan las variaciones de la variable (la pendiente de la gráfica) son cada vez menores y que por tanto los datos se parecen cada vez menos. Es una representación gráfica-matemática de la primera ley de la geografía de Tobler: «Todas las cosas están relacionadas entre sí, pero las cosas más próximas en el espacio tienen una relación mayor que las distantes. «
La gráfica resultante de la fórmula presentada previamente se conoce como variograma experimental, y lo normal es que acto seguido se realice un ajuste idealizado que normalmente tiene entre sus posibilidades un modelo esférico, exponencial, Gaussiano, Cúbico entre otros y que produce lo que se conoce como un variograma teórico.

Las principales características que definen un variograma teórico son:
- Alcance: Distancia a la cual el variograma se estabiliza
- Meseta: Valor constante que toma el variograma
- Pepita o nugget: intercepto con el eje «y» del variograma teórico. Que en teoría debería de ser cero (la variación de un valor respecto de sí mismo (h=0) es nula) pero por ajustes y errores en las mediciones casi siempre tiene un valor.
Como el variograma se realiza en una dirección determinada, al comparar los variogramas de varias direcciones se puede observar cómo es la variación de los datos en una dirección comparada con las otras. A ese fenómeno de diferencias de variación en función de la dirección se conoce como anisotropía.
Entonces, ¿Qué tiene que ver el Kriging y el variograma? La respuesta es que con el Kriging nosotros podemos visualizar la tendencia espacial de los datos y definirla a través de sus propiedades (meseta, alcance y pepita). Básicamente con esta información el Kriging no solo predice un valor en un punto sino que además nos dice cuál es la probabilidad de que ese punto tenga ese valor.
Así, con base en lo anterior el método de krigeado predice valores asignándole un peso a cada dato con base en el modelo de variograma teórico escogido. La idea es escoger el mejor modelo que resulte con la menor varianza, cosa que no es nada fácil y por eso muchos dicen que el Kriging es un arte porque hay que ir realizando una serie de ensayos prueba y error hasta escoger el mejor modelo posible.

Hay diferentes tipos de Krigeado pero no quiero empantanar aún más el tema y que se vuelva demasiado tedioso, hay muchas entradas en internet sobre cómo calcular el Kriging en software GIS e incluso a mano por lo que prefiero dejar el tema aquí para quizás en una futura entrada explicar en detalle cada uno de esos métodos.
Esperamos que esta entrada haya sido interesante para ti y que hayas aprendido mucho. Si hubiera alguna pregunta, no dudes en dejarla en los comentarios, más abajo o a través de nuestras redes sociales y a la mayor brevedad posible las estaremos respondiendo. Si esta entrada te ha gustado te invitamos a que la compartas para que este conocimiento llegue a más personas. Hasta la próxima
Otras entradas que te pueden interesar:
- Consultoría de catastro multifinalitario El Salvador
- ¿Qué es la Topología?
- Control de verticalidad con apoyo topográfico
- Usando LiDAR para descubrir sitios arqueológicos en El Salvador
- La costa salvadoreña en un mapa científico francés del siglo XVIII.
SOBRE EL AUTOR
ELLOS YA CONFÍAN EN NUESTRA EXPERIENCIA Y CALIDAD

DEJANOS TUS COMENTARIOS Y SÍGUENOS EN NUESTRAS REDES SOCIALES: