Técnicas de observación de la tierra (II): Geodesia

18 abril, 2019

Técnicas de observación de la tierra (II): Geodesia

A lo largo de la historia el hombre ha sentido la necesidad de representar la superficie terrestre y los objetos situados sobre ella. Hoy vamos a desglosar el segundo tópico de nuestra serie de observación de la tierra con un tema, que desde mi punto de vista personal, es uno de los más difíciles de la geomática. El artículo de hoy es extenso, denso y todavía aun así nos quedaremos cortos frente a una rama de la geomática que tira de la matemática pura y dura para poder expresarse.

En palabras sencillas, Geodesia es la ciencia que estudia la forma y tamaño de la tierra y las posiciones sobre la misma.

Básicamente la geodésica puede dividirse en tres grandes ramas:

Geodesia teórica. Que se encarga de la observación, descripción y análisis temporal del campo gravitatorio terrestre. La dirección del campo de gravedad y la dirección vertical no son idénticas. Cualquier superficie perpendicular a esta dirección es llamada superficie equipotencial. Una de estas superficies equipotenciales es el Geoide. El problema de la determinación de la figura terrestre es resuelto para un determinado momento si es conocido el campo de gravedad dentro de un sistema espacial de coordenadas.

Anomalías del campo gravitatorio terrestre

La geodesia define el geoide como una superficie en la que todos los puntos experimentan la misma atracción gravitatoria siendo esta equivalente a la experimentada al nivel del mar.

Geodesia física. La mayor parte de las mediciones geodésicas se aplica en la superficie terrestre, donde, para fines de determinaciones planimétricas, son marcados puntos de una red de triangulación. Con los métodos exactos de la Geodesia matemática se proyectan estos puntos en una superficie geométrica, que matemáticamente debe ser bien definida. Debido a la irregularidad de los materiales que componen la corteza y el manto terrestre el geoide es una figura irregular y para describir la forma de la tierra suelen utilizarse modelos de la misma denominados esferoides o elipsoides de referencia. Estos se definen mediante dos parámetros, el tamaño del semieje mayor y el tamaño del semieje menor.

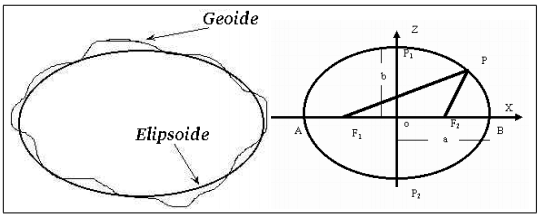
Representación del geoide y el elipsoide

Geodesia cartográfica. Para poder asignar coordenadas geográficas a los diferentes puntos de la superficie terrestre es necesario anclar el elipsoide al geoide mediante un punto fundamental en el que el elipsoide y el geoide son tangentes. De este modo el elipsoide se convierte en un sistema de referencia de la esfera terrestre.

Un datum geodésico es una referencia de las medidas tomadas. En geodesia un datum es un conjunto de puntos de referencia en la superficie terrestre con los cuales las medidas de la posición son tomadas y un modelo asociado de la forma de la tierra (elipsoide de referencia) para definir los sistemas de coordenadas geográfico. Datum horizontales son utilizados para describir un punto sobre la superficie terrestre. Datum verticales miden elevaciones o profundidades.

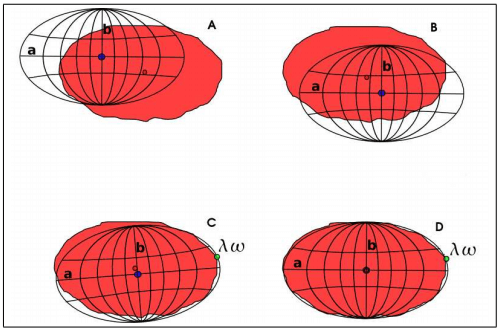
Los parámetros que definen un datum son los ejes mayor y menor del elipsoide, las coordenadas geográficas (latitud y longitud) del punto fundamental y la dirección del norte m

Un sistema de referencia geodésico es un recurso matemático que permite asignar coordenadas a puntos sobre la superficie terrestre. Son utilizados en geodesia, navegación, cartografía y sistemas globales de navegación por satélite para la correcta georreferenciación de elementos en la superficie terrestre. Estos sistemas son necesarios dado que la tierra no es una esfera perfecta. Dentro de estos cabe distinguir los llamados sistemas locales, que utilizan su definición un elipsoide determinado y un punto datum, los sistemas locales cuyos parámetros están dados por una terna rectangular cuyo origen se encuentra en el geocentro terrestre. Para definir las coordenadas geodésicas cuentan con un elipsoide de revolución asociado.

Ejemplos de algunos sistemas de referencia geodésico son:

WGS84, Sistema geodésico mundial que data de 1984
ED50, datum europeo de 1950
ETRS89, Sistema de referencia terrestre europeo de 1989
SIRGAS, Sistema de referencia geocéntrico para las Américas

El sistema de coordenadas natural de un esferoide y por tanto de un datum es el de coordenadas angulares (latitud y longitud) que suele denominarse coordenadas geográficas. Para definir latitud y longitud debemos identificar el eje de rotación terrestre. El plano perpendicular al eje de rotación que corta la tierra atravesándola por su centro define el Ecuador en su intersección con el esferoide. El resto de las líneas de intersección con la superficie terrestre de los infinitos planos perpendiculares al eje de rotación definen los paralelos o líneas de latitud constante. Finalmente, los meridianos pueden definirse como las líneas de intersección con la superficie terrestre de los infinitos planos que contienen al eje de rotación.

La longitud (λ) es la distancia angular entre el meridiano de un lugar y el de Greenwich, se expresa en grados, minutos y segundos de arco y se mide de 0° a 180° hacia el Este o hacia el Oeste desde el meridiano de Greenwich. La latitud (ω) es la distancia angular entre el paralelo de un lugar y el Ecuador, se expresa en las mismas unidades que la longitud y se mide de 0° a 90° hacia el Norte o el Sur. E

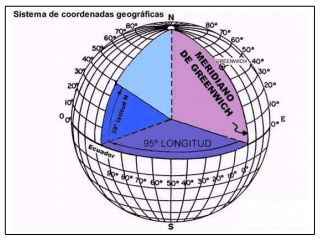
El proceso de transformar las coordenadas geográficas del esferoide en coordenadas planas para representar una parte de la superficie del elipsoide en dos dimensiones se conoce como proyección y es el campo de estudio tradicional de la ciencia cartográfica.

Sistemas de referencia más utilizados en Geodesia

Sistema global de coordenadas (cartesianas rectangulares)

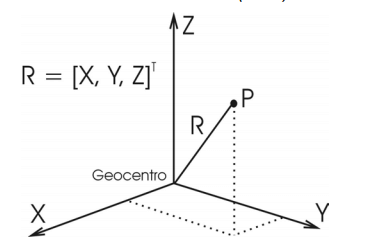
Marco de referencia para coordenadas cartesianas

Sistema: X, Y, Z
Origen: Geocentro
Eje Z: Eje de rotación terrestre
Eje X: Sobre el ecuador en dirección del meridiano de Greenwich

Sistema horizontal local de coordenadas (tangencial, local o topocéntrico)

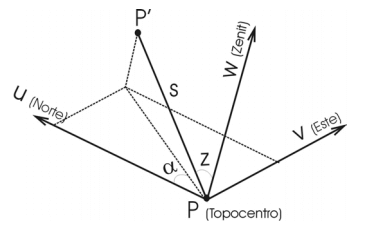
Marco de referencia para sistema topocéntrico de coordenadas

Sistema: N, E, U
Origen: Punto de observación (topocentro)
Eje u: Dirección Norte
Eje v: Dirección Este
Eje w: Tangente a la línea de la plomada en el punto de observación en dirección del cenit

Sistema de coordenadas curvilíneas (Elipsoidales o geodésicas)

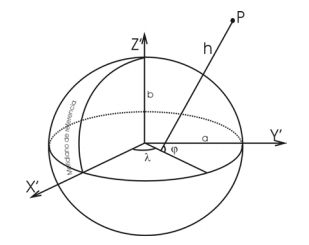
Marco de referencia para sistema geodésico de coordenadas

Sistema: Latitud φ, Longitud λ, Altura h
Origen: Centro geométrico del elipsoide
Eje Z: Eje menor del elipsoide en dirección del polo norte
Eje X: Sobre el plano ecuatorial en dirección del meridiano de referencia

Coordenadas planas (Proyecciones cartográficas)

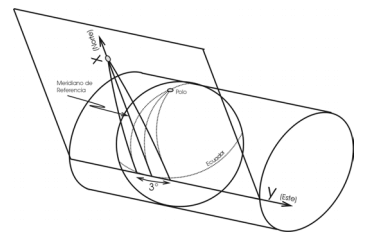
Sistema: X, Y, Z
Origen: meridiano de tangencia con paralelo de referencia
Eje X: Coordenada Norte
Eje Y: Coordenada Este

Tipos de proyección

El problema fundamental a la hora de abordar una proyección es que no existe modo alguno de representar en un plano toda la superficie del elipsoide sin deformarla, el objetivo va a ser minimizar, en la medida de los posible, estas deformaciones. Puesto que el efecto de la esfericidad de la superficie terrestre es proporcional al tamaño del área representada (y en consecuencia a la escala), estos problemas sólo se plantean al cartografiar zonas amplias. Cuando se trata de cartografiar zonas pequeñas, por ejemplo, una ciudad, la distorsión es despreciable por lo que se suelen utilizar coordenadas planas, relativas a un origen de coordenadas arbitrario y medidas sobre el terreno. A estas representaciones se les llama planos en lugar de mapas.

Cuando la distorsión debida a la esfericidad de la superficie terrestre se considera relevante se hace necesario buscar una ecuación que a cada par de coordenadas geográficas le asigne un par de coordenadas planas de manera que los diferentes elementos y objetos de la superficie terrestre puedan ser representados sobre un plano.

El foco de la proyección puede ubicarse en diferentes puntos dando lugar a diferentes tipos de proyecciones. De este modo podemos clasificar las proyecciones en función del objeto geométrico utilizado para proyectar se habla entonces de proyecciones cilíndricas, cónicas y azimutales o planas.

Una proyección implica siempre una distorsión en la superficie representada, el objetivo de la cartografía es minimizar estas distorsiones utilizando la técnica de proyección más adecuada a cada caso. Las propiedades del elipsoide que pueden mantenerse son:

Conformidad. Si un mapa mantiene los ángulos que dos líneas forman en la superficie terrestre, se dice que la proyección es conforme. El requerimiento para que haya conformidad es que en el mapa los meridianos y los paralelos se corten en ángulo recto y que la escala sea la misma en todas las direcciones alrededor de un punto, sea el punto que sea. Una proyección conforme mantiene además las formas de polígonos pequeños. Se trata de una propiedad fundamental en navegación.
Equivalencia. Es la condición por la cual una superficie en el plano de proyección tiene la misma superficie que en la esfera. La equivalencia no es posible sin deformar considerablemente los ángulos originales, por lo tanto, ninguna proyección puede ser equivalente y conforme a la vez. Resulta conveniente por ejemplo en planos catastrales.
Equidistancia. Cuando una proyección mantiene las distancias reales entre dos puntos situados sobre la superficie del Globo (representada por el arco de Círculo Máximo que las une).

La imagen anterior es un ejemplo de la determinación de coordenadas para un sistema de transformación, en este caso el de uso mas extendido: La proyección Transversal de Mercator (UTM). Sin embargo, a lo largo de la historia muchos cartógrafos han intentando resolver el problema de plasmar en un plano la casi esfericidad de la tierra.

PROYECCIÓN CILÍNDRICA: es la que se ejecuta sobre un cilindro que luego se extiende hasta formar un rectángulo. En ella los meridianos y paralelos se cruzan en ángulo recto.

A continuación se muestran dos proyecciones cilíndricas de dos cartógrafos distintos y utilizando conservación de propiedades diferentes, una es equivalente (conserva las áreas iguales) y la otra es conforme (conserva la forma):

Proyección cilíndrica equivalente de Peters

La tierra en una proyección cilíndrica conforme de Mercator

PROYECCIÓN CÓNICA: es la que se realiza sobre un cono cuyo centro es el Polo Norte o el Polo Sur. Tiende a exagerar las superficies hacia el ecuador. En ella los meridianos son rectas que convergen hacia el Polo y los meridianos son semicírculos con centro en dicho Polo.

Europa en una proyección cilíndrica de Lambert

PROYECCIÓN AZIMUTAL: es la que se plasma sobre un plano tangente a un punto de la superficie de la Tierra. No permite representar toda la Tierra, por lo que según sea la tangente puede ser: polar, ecuatorial u oblicua.

A continuación se presentan otros tipos de proyección de diferentes cartógrafos:

Como ven el tema de la Geodesia es un tema amplio y con mucha mucha matemática de por medio. He querido simplificar un poco las cosas pero si hubiera alguna duda dejala en los comentarios al pie de este post o en nuestras redes sociales y con gusto trataré de aclararlo.

No olvides compartir para que esta información llegue a más personas.